A continuacion se dan una serie de demostraciones de geometria

	Sign In Sign-Up

GEOMETRIA PLANA

By Enrique Camacho.

Para poder hacer demostraciones toma en cuenta los siguientes consejos:

Apunta todo lo que sabes de lo que te piden que demuestres, de esta manera podrás partir bien y llegar fácilmente a lo que quieres.
Saber atacar el problema, esto es cite piden demostrar que dos segmentos son iguales, demuestra que son parte de triángulos congruentes. También sabrás atacar un problema si sabes todo lo que tienes.
Si la figura es un poco rara y tu ni que onda, puedes, hacer trazos auxiliares. Estos por lo general son líneas que ayudan a formar triángulos, y de estas sacar bastante
La mayoría de los métodos de demostración de los maestros es algo fastidioso aunque así sea la manera correcta de demostrar el lo que te piden, lo mejor que puedes hacer es hacerlo a mi manera, es decir primero apuntas lo que sabes (todo sin excepción aunque sea muy obvio) y ver como atacar el problema.
Observa muy bien tu figura antes de empezar a resolverlo, aprende a descubrir lo que esta en tu figura por ejemplo. El ejercicio 1 hay dos triángulos iguales ,cosa que no te lo dicen pero ahí están es cosa de que tu lo veas.
Si de plano no ves ni que onda con Geometría ,no es un buen consejo pero algunos les funciona, pide le la libreta a alguno de los que si le entienden a esto sácale copia y apréndete las demostraciones de geometría no hay otra,(si quieres pasar la metería).
Apréndete los axiomas y teoremas mas usuales

Postulados de congruencia (estos te servirán para hallar segmentos , ángulos y triángulos iguales)

POSTULADO LAL :

Si en un triángulo se tienen dos lados y el ángulo comprendido entre dichos lados, iguales a los correspondientes elementos de otro triángulo, entonces los triángulos son congruentes

POSTULADO ALA :

Si en un triángulo se tienen dos ángulos y el lado comprendido entre dichos ángulos, iguales a los correspondientes elementos de otro triángulo, entonces los triángulos son congruentes

POSTULADO LLL :

Si en un triángulo sus tres lados son iguales a los correspondientes elementos de otro triángulo ,entonces los triángulos son congruentes

N mucho ojo:

No existen postulados como LLA ,ALL ,AAL ,LAA y sus posibles combinaciones ,solo existen esos tres postulados LAL , ALA y LLL .

1.-En el triángulo ABC <A=<B y <BAP = <ABQ. Demuéstrese que AP=BQ

Del triángulo BQA y PBA se puede sacar que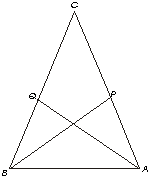

<A = <B

<QBA = <PAB

AB = AB

Por el postulado ALA son congruentes los triángulos

Por tanto BP=QA por ser lados congruentes de triángulos congruentes

2.- Suponiendo que AC = BC demuéstrese que los ángulos M y N son iguales

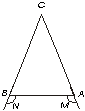
AC = BC lo que implica que <CBA = <CAB (a lados iguales se oponen ángulos iguales)

<M = <N por que los complementos de ángulos iguales son iguales

3.- En la figura P,Q,R son puntos medios de los lados de un triángulo equilátero ABC. Demuéstrese que PQR es equilátero

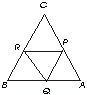<B = <A =C por ser ángulos de un triángulo equilátero

Por se P,Q y R puntos medios de los lados de un triángulo equilátero entonces

BR = CR = CP = PA = BQ = AQ.

Los triángulos BRQ , CRP , PQA son congruentes por ALA .

Por tanto PQ=QR=RP (por ser lados congruentes de triángulos congruentes)

Y así se demuestra que PQR es un triángulo equilátero.

4.- En el paralelogramo ACDB, AP = CR ,BQ = DS. Demuéstrese que PQRS tambien es un paralelogramo.

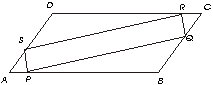En este problema lo mejor es encontrar triángulos congruentes y así relacionar lados del cuadrilátero que os piden demostrar que es un paralelogramo.

Sabemos: AD = BC , DC= AB

AP=CR , BQ = DS

AB= AP + PB Y DC = DR + CR

AP + PB = DR + CR è PB = DR

DA = DS + SA Y BC = QC + QB

DS + SA = QC + BQ è SA = QC

Observamos los triángulos PQB y SDR ,tienen en común:

BQ = DS, PB = DR y los ángulos <D = <B (los ángulos opuestos de un paralelos gramo son iguales)

è por el postulado LAL los triángulos son iguales ,lo que significa que SR = PQ

Lo mismo se hace para probar que los triángulos ASP y RQC son iguales y obtener que RQ = SP

Ahora que tenemos lo que queriamos SR = PQ y RQ = SP podemos utilizar el siguiente teorema para demostrar lo que nos piden:

" Si cada lado de un cuadrilátero es igual a su opuesto, el cuadrilátero es un paralelogramo"

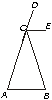5.- En todo triángulo isósceles, la bisectriz del ángulo externo opuesto a los ángulos iguales es paralela al lado desigual.

Sabemos:

Sean CA y BC los lados iguales de un triángulo isósceles

è <A = <B

Sea CE la bisectriz del ángulo externo BCD

è <BCD / 2 = DCE =BCE

Por ser BCD un ángulo externo sabemos que es igual a la i suma de los ángulos internos no adyacentes a el.

è <BCD = [ <A + <B ] = [ <A + <A ] = 2 <A

<A = <BCD /2 = DCE

Como <A = <DCE , CE es // a AB

6.- Si por un punto cualquiera de la bisectriz de un ángulo se traza una paralela a uno de los lados del ángulo ,el triángulo así formado es isósceles

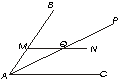
Sea AP la bisectriz del ángulo <BAC

è <BAP = <PAC

Sea MN la paralela a un de los ángulos

è < CAQ = < PQN por ser ángulos correspondientes

< AQM = < PQN por ser opuestos por el vértice

è AM = MQ a angulos igueles se oponen lados igules

y en este ultimo paso demostramos que AMQ es un triangulo isosceles

7.- En un paralelogramo ABCD, Q es el punto medio de AD y P el punto medio de CB. Demuestrese que BQ y DP trisectan AC.

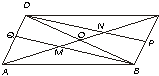
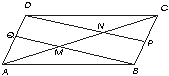Se hace un trazo auxiliar el c

segmento DB

Sabemos :

O es el punto medio de las diagonales CA y DB è AO = OC y DO = OB

DA = CB y DC = BA

P y Q son puntos medios

è DQ = QA = CP = PB

Los triángulos DBA y DBC son iguales

Observemos el triángulo DAB :

QB y AO son medianas que se cortan en M ,por tanto M es el baricentro, M tiene la propiedad de dividir a una mediana en 2/3 y en 1/3 el segmento, entonces en el segmento AO , AM son los 2/3 y MO es 1/3. Lo mismo pasaría para el triángulo DBC OC y DP serian medianas que se cortan en N, entonces en el segmento OC , NC es 2/3 y NO es 1/3 ,sumando la distancia MO y NO nos da 2/3

è AM = MN = NC

De esta manera queda demostrado que el segmento AC es trisecado

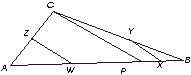8.- Sobre el lado AB de un triángulo ABC se toma un punto cualquiera P .Luego se hacen AW = WP ,PX = XB, AZ = ZC ,BY = YC .Demuestrese que XY = WZ

Los triángulos CAP y AZW son semejantes

Por tener proporcionales dos catetos y el ángulo comprendido igual.

AZ = ½ CA

AW = ½ AP

ZW = ½ CP

Lo mismos pasa con los triángulos CPB y Y XB

YB = ½ CB

XB = ½ PB

XY = ½ PB

è XY = ½ PB = ZW

Así queda demostrado que XY = ZW

9.- En la figura ,AC = BC ,AP,BQ,CR y CS son iguales. Demuestrese que PQ = RQ

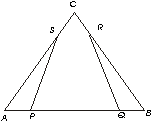
Sabemos que :

CA = BC

CA = SC + SA
BC = CR + RB
SC + SA = CR + RB è SA = RB

AP = QB dato

<A = <B a ángulos iguales se oponen lados iguales

Por el postulado ALA los triángulos APS y RQB son iguales.

Por lo tanto PQ = PS por ser lados congruentes de triángulos congruentes.

10.- Sobre los lados de un triángulo ABC se construyen los triángulos equiláteros BQC,CRA,APB. Demuestrese que las rectas AQ,BR,CP son iguales.

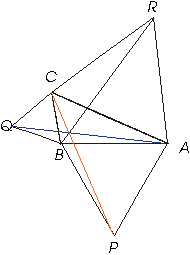Lo que nos piden demostrar es la igualdad de tres ineas, entonces esto podría implicar la igualdad de triángulos congruentes .

Observemos solo las líneas CP y BR

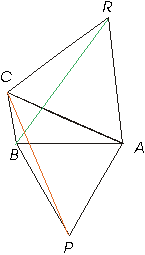Ahora demostraremos que RB = CP

Llamemos al ángulo CAB = a

Los ángulos CAR y PAB miden 60 grados por se ángulos de triángulos equiláteros.

El ángulo BAR = 60 + a

El ángulo CAP = 60 + a

è < BAR = < CAP

Observemos los triángulos CPA y ABR

Tienen en común:

AP = BA , CA = RA y < BAR = < CAP

Por el postulado LAL los triángulos CAR y PAB son iguales.

è CP = BR por se lados congruentes de fig. congruentes.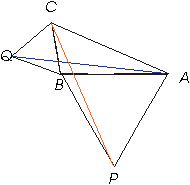

Ahora demostraremos que CP = QA

Lamemos al ángulo ABC = b

<CBQ = <ABP = 60 grados

< QBA = <CBQ + 60

< CBP = <ABP + 60

< QBA = <CBP

Observemos los triángulos CBP y QBA tienen en común.

CB = QB , BP = BA y < QBA = <CBP

Por el postulado LAL los triángulos CBP y QBA son iguales.

è CP = QA por se lados congruentes de fig. congruentes.

Ahora tenemos que CP = BR y CP = QA è CP = BR = QA

11.- Las bisectrices de dos ángulos externos de un triángulo cualquiera ABC se encuentran en P .Demuestrese que la suma del ángulo P y la mitad del A es igual a un recto.

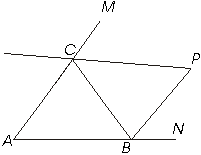Sea CP la bisectriz del ángulo externo MCB y BP la bisectriz del ángulo externo CBN

Llamemos al ángulo A = a al ángulo ABC = b y al ángulo ACB = f

Nos piden demostrar lo siguiente :

a /2 + <P = 90

Sabemos que :

b + a + f = 180 , <PCB = <MCB /2 , <CBP = CBN /2

< MCB = b + a , < CBN = a + f

<PCB + < CBP + < P = 180

<MCB /2 + CBN /2 + < P = 180

(b + a ) /2 + ( a + f ) /2 + < P = 180 è < P = 90 - a /2

Sustituyendo esto en lo que nos piden demostrar

a + <P = 90

a /2 + 90 - a /2 = 90

90 = 90